For billiards enthusiasts and those participating in pool tournaments, understanding the game’s intricacies is crucial. One such intricacy is mastering the art of aiming, which involves understanding the exact point to strike. This knowledge, often acquired through extensive practice, builds muscle memory over time. However, for amateurs or those looking to understand how to play pool angles, dedicating such time might not be feasible. Hence, a scientific and systematic study becomes essential.

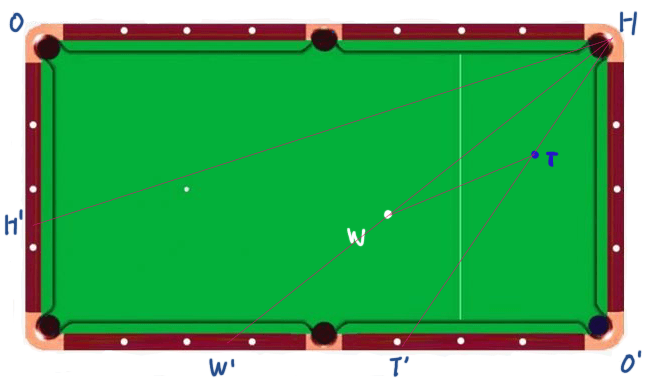
The image above illustrates the basic setup of a pool table. The challenge is to strike the white ball (W) in such a way that the target ball (T) goes into the hole (H). This involves calculating angles in pool, a skill that can be daunting for beginners. But with the right pool angle calculator or pool shot calculator, it becomes more manageable.

For those new to the game, understanding pool angles for beginners can be a game-changer. The positioning stars on the pool table, often referred to as the pool table angle chart, serve as reference points, helping in determining the pool ball angles.

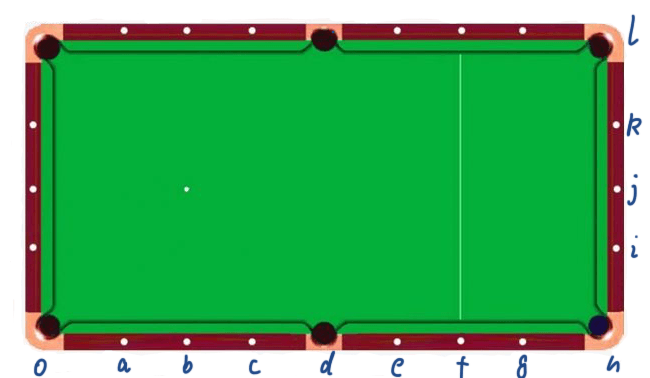
The distances between these positioning stars are consistent. The long side of the billiard table has 8 segments, and the short side has 4. This uniformity aids in calculating the angles:

∠glh = arctan(0.25) = 14 degrees
∠flh = arctan(0.5) = 27 degrees
∠elh = arctan(0.75) = 37 degrees
∠dlh = arctan(1) = 45 degrees
∠clh = arctan(1.25) = 51 degrees
∠blh = arctan(1.5) = 56 degrees
∠alh = arctan(1.75) = 60 degrees
∠olh = arctan(2) = 63 degrees

These 8 angles are enough to cover any angle change in billiards, so you need to remember.

Now let’s go back to the first picture and show how to calculate the angle of ∠WTH.

We can know by drawing an extension cord:

The extension point T of HT almost coincides with 37 position, so the ∠O’HT angle is 36 degrees.

The extension point W’ of HW is almost at the 51 position, so the ∠O’HW angle is 53 degrees.

Thus the ∠WHT angle is equal to 53-36 = 17 degrees.

We also need to draw a parallel line HH’ of WT.

H’ is almost a little more than two positioning stars. Compared with the long side, it is a little more than arctan (0.25).

From this, the angle of ∠OHH’ is estimated to be a little more than 14. Calculated 16 degrees.

Then the angle of ∠H’HW=90-16-53=21 degrees

From this, the∠WTH angle = 180-21-17 = 142 degrees

However, when we aim at it, we don’t need to calculate the obtuse angle. If we can directly calculate the acute angle, the ∠WTT’ angle is 21+17=38 degrees.

The angle is calculated. The next question is coming:

How do we aim at the 38 degree angle?

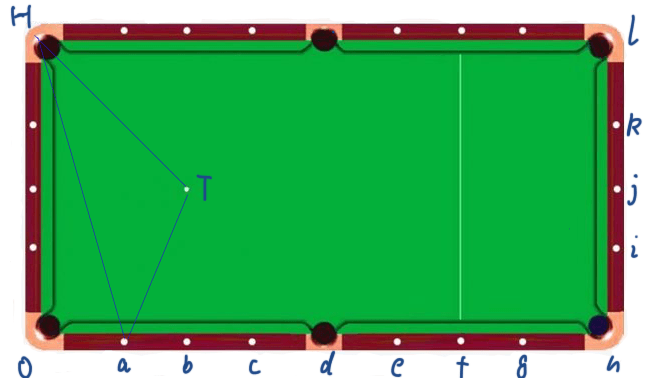
Another picture

The T point is the pendulum point, the ∠THO angle is 45 degrees, and the Tab angle is arctan (2) is 63 degreee.

Then you can know that the angle of ∠aTH is 63+45=108 degrees.

We converted it to an acute angle of 72 degrees.

In the same way, we calculate that point b is a 45-degree angle.

Point c is 63-45 = 18 degrees.

The d point is 0 degrees. No need to consider

The e point is 45-arctan (2/3) = 45-33 = 12 degrees

The point f is 45-arctan (2/4) = 45-27 = 18 degrees. Just like c, just aim from the other direction.

The g point is 45-arctan (2/5) = 45-22 = 23 degrees.

h point is 45-arctan(2/6)=45-18=27 degrees

The i point is 45-arctan (1/6) = 45-9 = 36 degrees

Version 2.0: The Ultimate 8 Ball Pool Angle Calculator

Two days after my initial post on how to get better at pool angles, I realized some shortcomings in my approach:

1. The angles calculated were based on the white ball, target ball, and the target hole. Given the diameter of the ball (5-6 cm), this could lead to significant errors.
2. The images used for illustration had two balls, but in actual aiming, the white ball isn’t present, making precise aiming challenging.

This led to the introduction of version 2.0, a more refined pool angles calculator.

Firstly, it’s essential to understand that the hole’s size is more than twice that of the ball. This means our aiming point is an area, not an exact spot.

From the image above, it’s evident that as long as the white ball strikes the small triangular area drawn, the target ball can enter the hole.

In addition to the long side’s positioning stars, the short side also offers several reference points:

Several angles caused by rearranging the short sides from small to large"

∠iOh= arctan(1/8) = 7 degrees

∠jOh= arctan (2/8) = 14 degrees

∠kOh= arctan (3/8)= 21 degrees

∠lOh= arctan (4/8) = 27 degrees

Several angles caused by the long side:

∠glh= arctan (0.25)= 14 degrees

∠flh= arctan (0.5)= 27 degrees

∠elh= arctan (0.75)= 37 degrees

∠dlh= arctan(1)= 45 degrees

∠clh= arctan(1.25)= 51 degrees

∠blh= arctan (1.5)= 56 degrees

∠alh= arctan(1.75)= 60 degrees

∠olh= arctan (2)= 63 degrees The next challenge is to quickly calculate these angles:

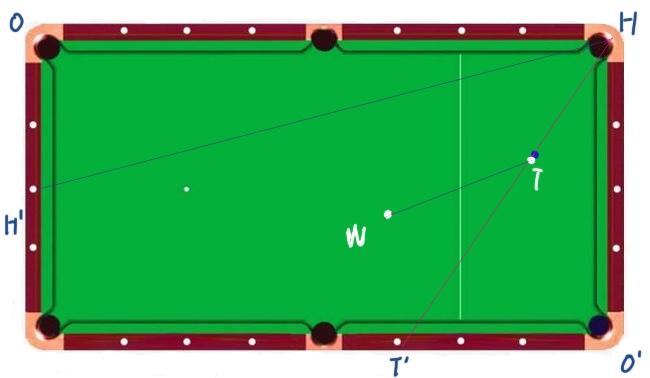
This version focuses on the angle ∠WTT, which involves a virtual white ball (T). In practice, you can align the cue stick along the target ball and the target hole, then determine the position of T.

In reality, you can take the rod along the target ball and the target hole, then get T “in which positioning star.

Visually check T “points in the long-side “37” position, then

∠O’HT= 36 degrees

Take the rod along the target hole and draw a parallel line H’H with the WT line.

H” point on the short side of “14” position, then

∠OHH” = 14 degrees

Then we have to calculate the angle:

∠WTT"= 90-36-14 = 40 degrees

A slight difference from the 38 degrees calculated in version 1.0.

Ok, there is no problem with the calculation angle. Now let’s retake the angle of each star in the picture below.

Version 1.0 has calculated the sharp angles of the points and defects for each point:

The a point is 72 degrees.

The b point is 45 degrees.

The c point is 63-45 = 18 degrees.

The d point is 0 degrees. No need to consider

The e point is 45-arctan (2/3) = 45-33 = 12 degrees

The point f is 45-arctan (2/4) = 45-27 = 18 degrees. Just like c, just aim from the other direction.

The g point is 45-arctan (2/5) = 45-22 = 23 degrees.

h point is 45-arctan(2/6)=45-18=27 degrees

The i point is 45-arctan (1/6) = 45-9 = 36 degrees

This time we need to put the white ball on the pendulum point and the black ball on the HT line, so that we can enter the hole by aiming at the ball.

Take real photos from each point:

This time, I will add a picture of about 60 degrees, because I jumped from 45 degrees to 72 degrees, and there is no more degrees in the middle.

With this updated approach, I hope to provide a more accurate and practical guide to mastering billiard angles. If you have suggestions or feedback, please share in the comments!

Related Articles:

• 2018/09/20   How to Calculate What Angle to Hit a Pool Ball Version 2.0