The day before yesterday I wrote Show How to calculate what angle to hit a pool ball with Real Photos, after two days of actual operation, I feel that there are some shortcomings.

First: the angle is the calculation of the white ball, the target ball and the target hole. Considering that the diameter of the ball is 5-6 cm, the calculated error will be larger.

Second: The picture of the angle ball is two balls, but when actually aiming, the white ball does not exist, and it is not easy to aim more accurately.

Therefore, I rethought and introduced this version 2.0.

First clarify a few basic concepts:

The hole is more than twice as big as the ball. I measured a few side holes, the hole opened 11 cm, and the hole in the hole opened 13 cm. And for a ball with a diameter of only 5-6 cm, our aim is an area, not a precise point.

 



As seen from the above picture, as long as the white ball knocks down the small triangle area drawn, the target ball can be hit into the hole.

In addition, the previous post has fewer memories of the positioning star. There are also several positioning stars on the short side that can also be used as a reference.



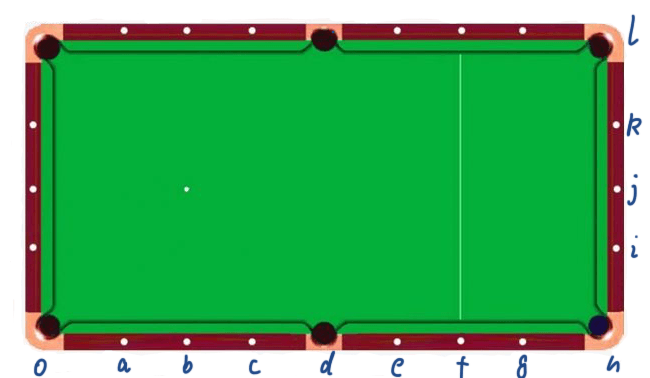
Several angles caused by rearranging the short sides from small to large"

∠iOh= arctan(1/8) = 7 degrees

∠jOh= arctan (2/8) = 14 degrees

∠kOh= arctan (3/8)= 21 degrees

∠lOh= arctan (4/8) = 27 degrees

Several angles caused by the long side:

∠glh= arctan (0.25)= 14 degrees

∠flh= arctan (0.5)= 27 degrees

∠elh= arctan (0.75)= 37 degrees

∠dlh= arctan(1)= 45 degrees

∠clh= arctan(1.25)= 51 degrees

∠blh= arctan (1.5)= 56 degrees

∠alh= arctan(1.75)= 60 degrees

∠olh= arctan (2)= 63 degrees

 

The next question is how to calculate the angle quickly.



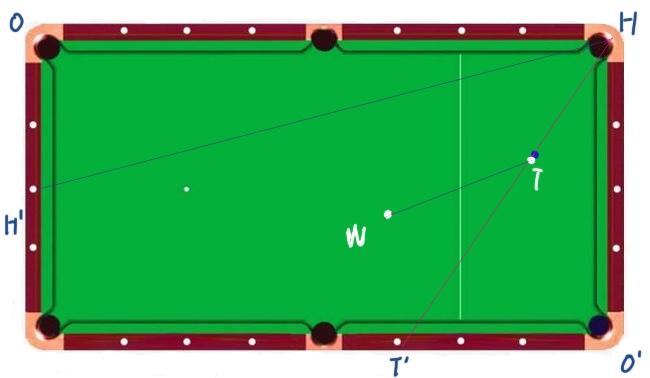
This version of 2.0 is not a white ball - the target ball - the angle of the hole. This time draw a virtual white ball T, this time we calculate the degree of ∠WTT.

In reality, you can take the rod along the target ball and the target hole, then get T "in which positioning star.

Visually check T "points in the long-side "37" position, then

∠O'HT= 36 degrees

Take the rod along the target hole and draw a parallel line H'H with the WT line.

H" point on the short side of "14" position, then

∠OHH" = 14 degrees

Then we have to calculate the angle:

∠WTT"= 90-36-14 = 40 degrees

A slight difference from the 38 degrees calculated in version 1.0.

Ok, there is no problem with the calculation angle. Now let's retake the angle of each star in the picture below.



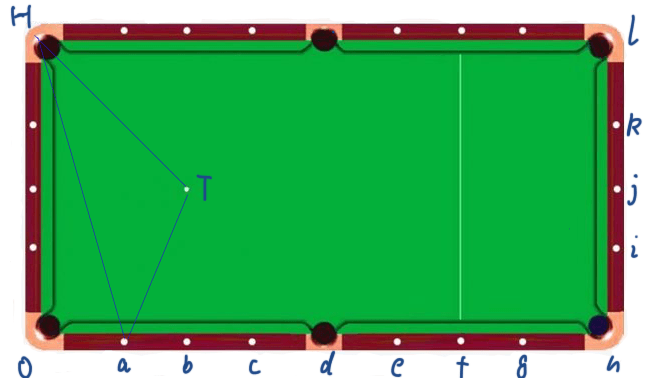
Version 1.0 has calculated the sharp angles of the points and defects for each point:

The a point is 72 degrees.

The b point is 45 degrees.

The c point is 63-45 = 18 degrees.

The d point is 0 degrees. No need to consider

The e point is 45-arctan (2/3) = 45-33 = 12 degrees

The point f is 45-arctan (2/4) = 45-27 = 18 degrees. Just like c, just aim from the other direction.

The g point is 45-arctan (2/5) = 45-22 = 23 degrees.

h point is 45-arctan(2/6)=45-18=27 degrees

The i point is 45-arctan (1/6) = 45-9 = 36 degrees

 

This time we need to put the white ball on the pendulum point and the black ball on the HT line, so that we can enter the hole by aiming at the ball.



Take real photos from each point:

 



 



 



 



 



 



 



This time, I will add a picture of about 60 degrees, because I jumped from 45 degrees to 72 degrees, and there is no more degrees in the middle.

 



Now the 2.0 version is updated.

If you have any better suggestions or criticisms, feel free to post your comment. :-)

 

 

 

Related Articles:

• 2018/09/18   Show How to calculate what angle to hit a pool ball with Real Photos